이 글은 PC 버전 TISTORY에 최적화 되어있습니다.
포스팅 순서
1. 개념 및 구현3. 구현 및 최적화
서론
1. 탐색 영역 둘러보기2. 탐색 시작3. 경로 채점4. 계속 탐색하기5. A* 알고리즘 요약
탐색 영역 둘러보기 (The Search Area)
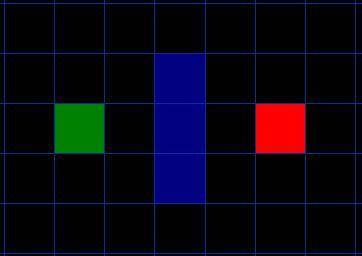
자, 간단하게 우리가 길을 찾아야할 지역을 탐색해보도록 하겠습니다. A지점에서 B지점으로 가는 것으로 목표가 정해졌습니다. 두 포인트 사이에 벽이 있네요. 이 가정은 아래 그림과 같습니다. 초록색은 시작포인트 A, 빨간색은 엔딩포인트 B입니다. 그리고 파란색으로 두 지점 사이에 벽이 쳐져있습니다.
그림을 보면 우리의 탐색 지역은 네모난 그리드로 나누어져있습니다. 위와 같이 탐색 지역을 단순화 하는 것이 첫번째 단계입니다. 이렇게 하면 우리의 탐색 영역은 2차원 배열로 줄어들게 되죠. 배열의 각 항목은 사각형이며 사각형은 이동 가능 또는 이동 불가능으로 나누어집니다. A* 를 통해서 어느 사각형들을 거쳐야하는지 파악함으로서 길을 찾는 것이죠. 경로가 발견되면 목표 도달 때 까지 사각형 중심에서 다음 사각형의 중심으로 이동합니다. 이 중심점들은 '노드'라고 부르겠습니다. (어떤 포스팅이든 노드라고 부르고 있으니 걱정마세요.)
탐색 시작 (Starting the Search)
성능 저하를 막기 위해 관기 가능한 노드 수로 단순화한 그리드 레이아웃(사각형들로 이루어진 레이아웃)을 만들었습니다. 그 다음 단계는 최단 경로를 찾기 위해 탐색을 시작해야겠죠. A점으로부터 B점까지 인접 사각형을 확인하면서 길을 만들어나가겠습니다. 아래의 순서로 스타트를 끊어봅시다.
- 시작점 A를 '열린 목록'에 넣어주세요. 이 목록은 일종의 장바구니와 같습니다. 지금은 시작점만 들어있지만 점점 많아질 것 입니다.
- 시작점에 인접한 벽, 물, 또는 위험 지형은 무시하고 지나갈 수 있는 사각형을 '열린 목록'에 넣어줍니다. 이 사각형들은 시작점 A를 부모로 지정합니다. ('부모 사각형'은 길을 다 찾고 거슬로 올라갈 때 중요한 것만 일단 기억해주세요.)
- '열린 목록'에서 시작점 A 사각형을 삭제하고 다시 볼 필요 없는 '닫힌 목록'에 추가해주세요.
그럼 위와 같은 그림이 나오게 됩니다. 녹색 사각형은 스타트 포인트입니다. 하늘색 선으로 둘러쌓여있다는 것은 이제 그 사각형은 '닫힌 목록'에 버려졌으니 다시 볼 필요 없다는 뜻입니다. 인접한 8개의 사각형은 밝은 녹색으로 윤곽선이 그려져 있죠. '열린 목록'에 들어가있다는 뜻입니다. 그리고 각각 회색 포인트로 부모 노드를 가리키고 있습니다.
자 이제, 우리는 '열린 목록'에 있는 사각형들 중에 하나를 선택해서 위의 순서로 반복 처리를 하게됩니다. 그럼 어떤 사각형을 선택해야할까요 바로 가장 작은 비용 F를 가진 사각형입니다. (F가 뭔지는 바로 아래서 설명하도록 하겠습니다.)
경로 채점 (Path Scoring)
자 어떤 사각형을 골라야할 까요? 그 키 포인트는 바로 다음 공식입니다.
F = G + H
- G - 시작점 A로부터 현재 사각형까지의 경로를 따라 이동하는데 소요되는 비용입니다.
- H - 현재 사각형에서 목적지 B까지의 예상 이동 비용입니다. 사이에 벽, 물 등으로 인해 실제 거리는 알지 못합니다. 그들을 무시하고 예상 거리를 산출합니다. 여러 방법이 있지만, 이 포스팅에서는 대각선 이동을 생각하지 않고, 가로 또는 세로로 이동하는 비용만 계산합니다.
- F - 현재까지 이동하는데 걸린 비용과 예상 비용을 합친 총 비용입니다.
위에서 설명한 것처럼 G는 사각형에 도착하기 위해 생성 된 경로를 사용하여 시작 지점에서 지정된 사각형으로 이동하는 데 드는 이동 비용입니다. 이 예에서는 수직, 수평 이동에 대해선 10, 대각선 이동에 대해서는 14의 비용을 할당합니다. 대각선으로 이동하는 실제 거리는 피타고라스 공식으로 수평 또는 수직 이동 비용의 약 1.414 배이기 때문에 간단히 14를 사용합시다. 이와 같은 정수를 사용하는 것은 컴퓨터에서 훨씬 빠르니까요. 그렇다면 현재 사각형의 G 비용 계산은 어떻게 해야하나요? 간단합니다. 현재 사각형의 회색 포인터가 가리키고 있는 부모의 G비용에 수평, 수직 이동이면 10을 더하고 대각선 이동이면 14를 더하면 됩니다.
H는 다양한 방식으로 추정 할 수 있습니다. 여기서 사용하는 방법은 맨하탄 (Manhattan) 방법이라고합니다. 이 방법은 현재 사각형에서 대상 사각형에 도달하기 위해 대각선 운동과 장애물은 무시하고 수평, 수직 이동 비용만 계산합니다. 어떤 사각형에서 목표까지 수평, 수직 이동의 개수에 10을 더하면 되는 것이죠. H(휴리스틱스)의 다른 방식에 대해서는 여기에서 찾을 수 있습니다.
F는 G와 H를 더하여 계산됩니다. 검색의 첫 번째 단계의 결과는 아래 그림에서 볼 수 있습니다. F, G, H 점수는 각 사각형에 표기됩니다. 시작 사각형의 바로 오른쪽에있는 사각형에서와 같이 F가 왼쪽 상단에 인쇄되고 G는 왼쪽 하단에 인쇄되고 H는 오른쪽 하단에 인쇄됩니다. 이 공식을 통해서 어떤 경로가 가장 비용이 싼지 '채점' 하는 것입니다.
이 방법을 통해 어떻게 생성된 것인지 자세하게 봅시다. 스타팅 포인트인 녹색 사각형 오른쪽의 사각형은 어떻게 F = 40, G = 10, H = 30이라는 숫자가 나왔을까요?
G는 스타팅 포인트로부터 수평으로 1칸 이동했으니 10, H는 현재 사각형으로부터 목표 포인트까지 수평으로 3번 이동했으니 10을 곱해 30이 되는 것 입니다. 총 합 비용인 F는 10 + 30 = 40인 것이죠.
자 이번에는 녹색 사각형 오른쪽 위를 봅시다. G는 스타팅 포인트로부터 대각선 방향에 있으므로 14입니다. (대각선은 무시하기로 했다구요? G는 시작 위치로부터 현재 위치의 실제 거리를 알기 때문에 대각선을 포함하여 계산합니다.) H는 4칸 이동이므로 40입니다. F는 총 합이니 54가 되겠죠.
계속 탐색하기 (Continuing the Search)
계속 탐색하기 위해서, '열린 목록'에서 가장 작은 F 비용을 가지고 있는 사각형을 선택합니다. 그리곤 아래의 스텝을 따라주면 됩니다.
1. 선택한 사각형을 '열린 목록'에서 빼고 '닫힌 목록'에 넣어주세요.
2. 인접한 사각형을 확인합니다. '닫힌 목록'에 있거나 벽은 무시하고 '열린 목록'에 사각형이 없다면 '열린 목록'에 추가해줍니다. 현재 사각형을 새로운 사각형의 '부모'로 지정합니다.
3. 인접한 사각형이 이미 '열린 목록'에 있다면 해당 사각형의 비용이 더 좋은지 확인합니다. 즉,선택한 사각형과 비교하여 G점수가 어떤 것이 더 낮은지 확인 합니다. 그렇지 않으면 아무것도 하지 않습니다. 하지만 해당 사각형의 G 비용이 더 낮은 경우 인접 사각형들의 부모를 새로운 사각형으로 바꿉니다. 마지막으로, 그 사각형의 F와 G를 다시 계산합니다. 어렵다면 아래의 실제 작업 과정을 봐주세요.


이번에도 마찬가지로 선택한 사각형의 오른쪽과 오른쪽 상단에 있는 벽은 무시합니다. 또한 벽 아래의 사각형도 무시합니다. (개발 방법마다 다르지만, 현재 사각형에서 벽 아래로 이동하려면 사각형이 대각선 모양으로 잘려야 부딪히지 않으므로 제외합니다.) 이제 남은 5개의 사각형을 보도록 하겠습니다. 좌측 상단, 상단의 사각형은 이미 '닫힌 목록'에 있으므로 무시합니다. 왼쪽 사각형은 '열린 목록'이므로 G 값을 통해 비교합니다. G 값이 더 낮으므로 넘어갑니다. 그리고 좌측 하단, 하단의 사각형을 '열린 목록'에 넣습니다. 이 같은 과정을 반복합니다.

선택 사각형 아래 왼쪽에 있는 사각형의 화살표가 이전과 바뀌었음을 주의해서 봐주세요. 이전의 G 값은 28이었으나 지금은 20이고 위쪽 사각형을 가리키고 있습니다. 이전과 같이 더 적은 비용 검사를 통해 부모가 바뀌고, G, F 비용이 다시 계산 된 것 입니다. 자 이것을 반복하면 아래와 같은 그림이 완성되고 엔딩 포인트에서 스타팅 포인트가 나올 때까지 부모를 따라갑니다. 이 경로가 최단 거리가 되는 것입니다. (아래 그림에서 빨간 점)
A* 알고리즘 요약
1. 시작사각형에서 검색된 인접사각형들을 열린목록에 넣습니다.
2. 다음의 과정들을 반복합니다.
ㄱ. 열린목록에서 가장 낮은 F 비용을 찾아 현재사각형으로 선택합니다.
ㄴ. 이것을 열린목록에서 꺼내 닫힌목록으로 넣습니다.
ㄷ. 선택한 사각형에 인접한 8 개의 사각형에 대해 탐색합니다.
- 만약 인접한 사각형이 갈수 없는 벽 이거나 그것이 '닫힌목록' 상에 있다면 무시, 그렇지 않은것은 다음을 계속합니다.
- 만약 이것이 '열린 목록'에 있지 않다면, 이것을 열린목록에 추가하고. 이 사각형의 부모를 현재 사각형으로 만듭니다. 사각형의 F,G,H 비용을 기록.
- 만약 이것이 이미 '열린 목록'에 있다면, G비용을 이용하여 이 사각형이 더 나은가 알아보고, 그것의 G비용이 더 작으면 그것이 더 나은 길이라는 것을 의미하므로 부모 사각형을 그 (G비용이 더 작은)사각형으로 바꿉니다, 그리고 그 사각형의 G,F비용을 다시 계산합니다.
ㄹ. 그만해야 할 때
- 길을 찾는 중 목표사각형을 '열린 목록'에 추가했을 때,
- '열린 목록'이 비어있게 될 경우.
(이때는 목표사각형을 찾는데 실패한것인데 이 경우 길이 없는 경우다.)
3. 길 저장하기.
목표 사각형으로부터 각각의 사각형의 부모사각형을 향하여 시작사각형에 도착할때까지 거슬러 올라갑니다.
참고 사이트
- A* Pathfinding for Beginners by Patrick Lester (Updated July 18, 2005)
- A* Pathfinding 구현
- A* Pathfinfing 발전 (어떻게 더 자연스러운 길찾기를 할 것인가?)
'Basic > 알고리즘' 카테고리의 다른 글
| A*(A star) 알고리즘 수도 코드(pseudocode) (0) | 2017.06.15 |
|---|